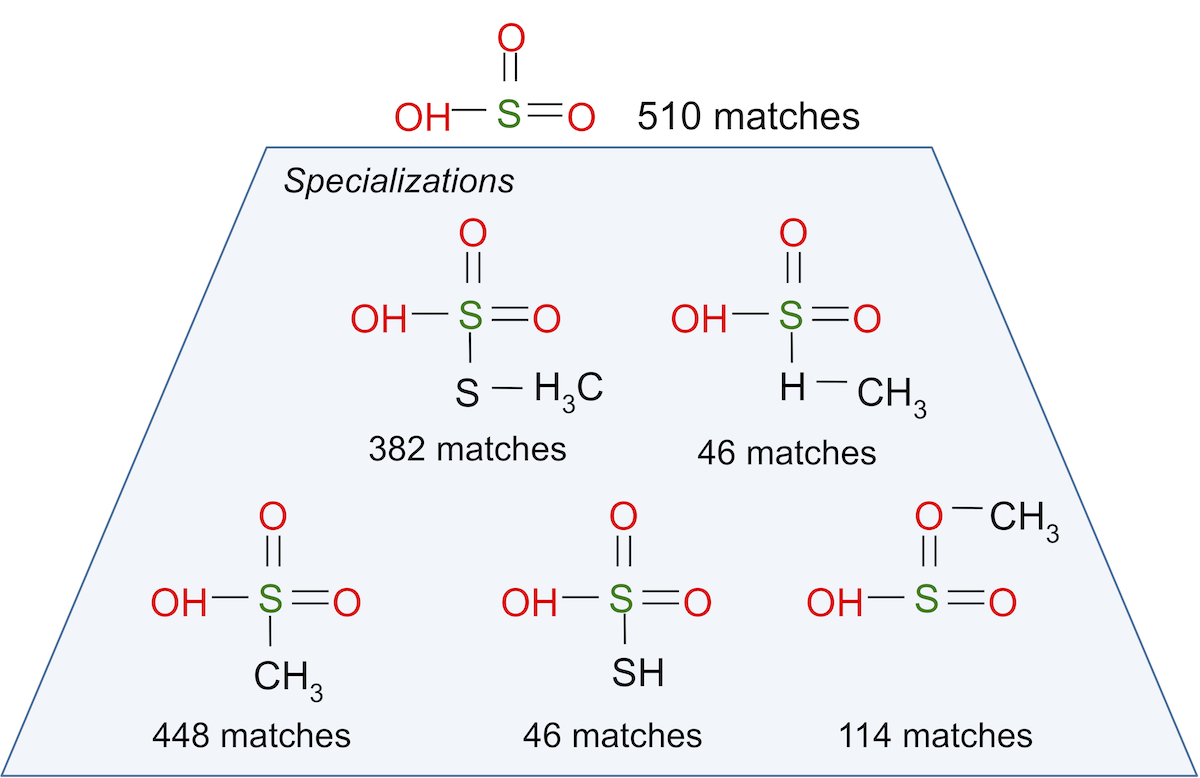
How can we find convenient reformulations?
TL;DR
Refinement of graph queries with
- \(\frac{1}{2}\)-approximate algorithm
- Informative reformulations with coverage and diversity
- Fast exact branch-and-bound heuristic for marginal gain
- Multiple experiments on real and synthetic datasets
Abstract
We study a problem of graph-query reformulation enabling explorative query-driven discovery in graph databases. Given a query issued by the user, the system, apart from returning the result patterns, also proposes a number of specializations (i.e., supergraphs) of the original query to facilitate the exploration of the results. We formalize the problem of finding a set of reformulations of the input query by maximizing a linear combination of coverage (of the original query’s answer set) and diversity among the specializations. We prove that our problem is hard, but also that a simple
The most challenging step of the greedy algorithm is the computation of the specialization that brings the maximum increment to the objective function. To efficiently solve this step, we show how to compute the objective-function increment of a specialization linearly in the number of its results and derive an upper bound that we exploit to devise an efficient search-space visiting strategy. An extensive evaluation on real and synthetic databases attests high efficiency and accuracy of our proposal

Share this post
Reddit
LinkedIn
Email